Glowworms

Memory limit: 128 MB

Early morning Byteasar woke up and went fishing in the Bytic Lake. At some moment he spotted a group of glowworms that were flying above the surface of the lake. Byteasar really enjoyed this view and decided to take a photo of the glowworms.

Photos made by Byteasar's camera have the shape of a square. Before a photo is taken, Byteasar decides on the vertical and horizontal alignment of the photo and zooms in or out. He never rotates the camera, otherwise the photo would turn out crooked.

Byteasar wants all the glowworms to be on the photo. He would like to adjust the parameters of the photo, in particular the camera zoom, so that the glowworms appear as big as possible. He is even willing to wait for a while until the glowworms form the best configuration for the photo to be taken.

We simplify things a bit and assume that all the glowworms are flying in a plane that is parallel to the camera sensor and that each glowworm has a constant velocity vector.

Input

The first line of input contains one integer (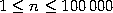), the number of glowworms. Each of the following lines contains four integers 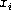, , 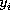, 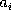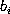(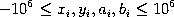) that represent the initial position 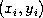and the velocity vector 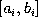of the 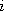-th glowworm. In other words, after 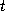units of time the 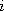-th glowworm has coordinates 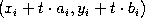. All points are specified in a rectangular coordinate system with axes parallel to the sides of the camera sensor.

Output

Your program should output one line with a non-negative real number - the minimal side length of a square that can be used to cover all the glowworms at some moment of time (the sides of the square must be parallel to the axes of the coordinate system). Your result may differ from the exact result by at most .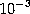

Example

For the input data:

4
4 0 -1 1
1 6 -1 -2
-1 -5 0 2
-1 -1 1 1

the correct result is:

3.00000000000000000000

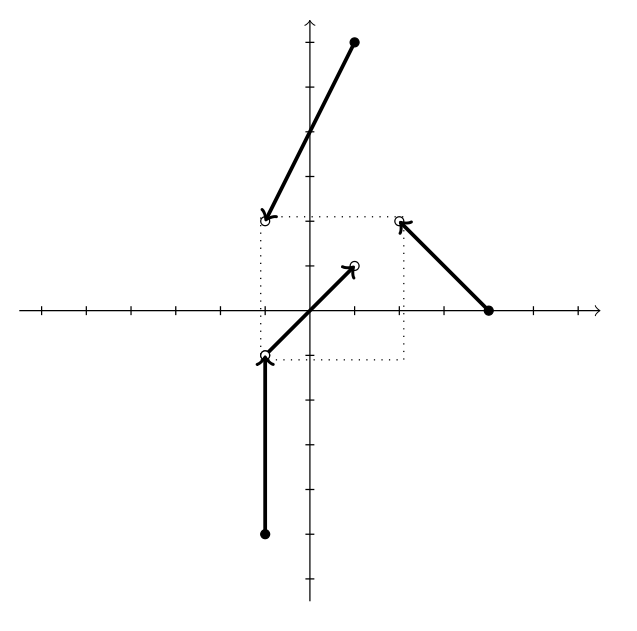
Explanation of the example: The figure shows the initial positions of the glowworms and their positions after 2 units of time. A 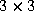square that covers all the glowworms at the time 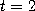is also shown. \end{minipage} \begin{minipage}{8cm}